Proof and Construction of Walker's Equation
Number 1 the mother of all Rational Numbers
I give the following equation, as the reason for calling the value of 1 {Quantity one} as the mother and
Sum of all possible Rational Numbers.
The Proof and derivation of the Relationship called " Walker's Equation " is given below.
as found and proposed by Wg Cdr Thomas Walker in 1998.
The greatness of this relationship is the fact that it shows that number 'one' 1is the sum of sums of all possible inverse powers of all possible positive integers that come after 1. That is, from ‘2’ to ‘ infinity’.

When expanded it becomes:
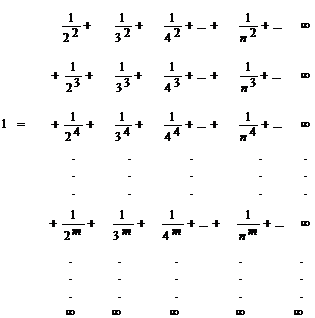
Given below is the simple derivation as to how I have derived this by my own independent analysis and finding.
The basis function used is the Binomial Theorem:
(1-n)-1 = 1 + n + n2 + n3 + n4 + . . .
Applying this we have :
(1- 1/2))-1 = 1 + 1/2 + 1/22+ 1/23+ 1/24+ . . .
2 = 1 + 1/2 + 1/22+ 1/23+ 1/24+ . . .
Therefore 1 = 1/2 + 1/22+ 1/23+ 1/24+ . . .
(1- 1/3))-1 = 1 + 1/3 + 1/32+ 1/33+ 1/34+ . . .
3/2 = 1 + 1/3 + 1/32+ 1/33+ 1/34+ . . .
Therefore 1/2 = 1/3 + 1/32+ 1/33+ 1/34+ . . .
(1- 1/4))-1 = 1 + 1/4 + 1/42+ 1/43+ 1/44+ . . .
4/3 = 1 + 1/4 + 1/42+ 1/43+ 1/44+ . . .
Therefore 1/3 = 1/4 + 1/42+ 1/43+ 1/44+ . . .
Similarly we have :
1/4 = 1/5 + 1/52 + 1/53 + 1/54+ . . .
1/5 = 1/6 + 1/62+ 1/63+ 1/64+ . . .
1/6 = 1/7+ 1/72+ 1/73+ 1/74+ . . .
1/7 = 1/8 + 1/82+ 1/83+ 1/84+ . . .
1/8 = 1/9 + 1/92+ 1/93+ 1/94+ . . .
So, this is how we construct Walker’s Equation:
1 = 1/2 + 1/22+ 1/23+ 1/24+ . . .
1/2 = 1/3 + 1/32+ 1/33+ 1/34+ . . .
1/3 = 1/4 + 1/42+ 1/43+ 1/44+ . . .
1/4 = 1/5 + 1/52+ 1/53+ 1/54+ . . .
1/5 = 1/6 + 1/62+ 1/63+ 1/64+ . . .
1/6 = 1/7 + 1/72+ 1/73+ 1/74+ . . .
1/7 = 1/8 + 1/82+ 1/83+ 1/84+ . . .
1/8 = 1/9 + 1/92+ 1/93+ 1/94 + . . .
As we substitute as indicated above all green colored terms vanish and we are left with only the terms which appear in the Walker’s Equation.
Hence Walker’s Equation is proved and constructed from fundamentals.
